Transformer from Scratch

In this blog I document my experience implementing the Encoder-Decoder Transformer base model from the famous work Attention is All You Need by Vaswani et al. My goal was to reimplement it as closely as possible to the original, from scratch, and without looking at their codebase tensor2tensor until absolutely necessary. The repo is available here.

Ultimately I had to consult the codebase and also make one major architectural change (Post-LN to Pre-LN). In addition, I used the HuggingFace tokenizer library to train a tokenizer and pre-process the dataset, rather than the older code from the moses repository. Initially, I started the implementation in PyTorch and pytorch_xla, but switched to Jax / Haiku midway through. I also used their original Bleu score evaluation function so as to be sure I was evaluating using the same metric.

I managed to reproduce the results of the base model in the paper to within very small margin. Evaluating on the 3000 sentence newstest2013 dataset, they achieve 4.92 and Bleu score 25.8 for their 65M parameter base model, after training for 100K steps. My implementation achieved PPL 4.95 and Bleu score 25.5 at that checkpoint.

Colab setup

Google Colab makes TPU v3 freely available for runs that usually last 12 hours or more. One can also pay for v4 and v5 TPU instances that can run later versions of jax, and either pre-emptible (meaning, it can shut off at any moment) (around $3 / hr) or not (~ $7 / hr). For my budget, especially for many dozens of 12 hour training run re-attempts, the free one was the right price! On the free Colab TPU, the model does train very fast. On the 4.5 M sentence pair English-German dataset, the model reaches the published Bleu score of around 25 after only 6-12 hours of training.

The colab notebook for training this model on TPU is available here. Google Colab on TPU only supports jax==0.3.25. The default image is pre-installed with jax==0.3.25, jaxlib==0.3.25 and flax==0.6.11
But, flax 0.6.11 actually requires jax>=0.4.2 as a dependency, see here.

Based on this advice and others, I settled on flax==0.6.4. I also used orbax for checkpointing, and only version 0.1.0 works. Although the orbax project currently recommends installing orbax-checkpoint rather than orbax for this, but this doesn't work in this case.

The final incantation is:

!pip install flax==0.6.4 jax==0.3.25 jaxlib==0.3.25 orbax==0.1.0

A runtime restart (Ctrl-M .) is required after installing this repo. Following this, if you want to use Google Cloud Storage and gs:// URLS to access your training dataset, you need to first authenticate the notebook to your Google account with:

!gcloud config set project PROJECT_ID

from google.colab import auth
auth.authenticate_user()

using a PROJECT_ID that has enabled Google Cloud Storage

The main cell invokes the train function directly as:

aiayn.train.main(
     'arch,reg,train,data,logging',
     ...

I also tried running it as:

python3 aiayn/train.py ...

but that does not work and I'm not sure why.

Data Pipeline

Tokenizer Training

In attempting to reproduce the tokenization in the original paper, I found the original codebase impractically slow. HuggingFace has reimplemented many tokenizer tools in Rust, and they are very nice and easy to use. The following is the excerpt for training a BytePair Encoded tokenizer.

The tricky part is to use bytes.decode on the elements in the Tensorflow DataSet using np.vectorize on batches. The batch size is arbitrary as long as it is sufficient to achieve good speed up. This function takes only about two minutes to complete.

from tokenizers import Tokenizer
from tokenizers.models import BPE
from tokenizers.normalizers import BertNormalizer
from tokenizers import pre_tokenizers
from tokenizers.trainers import BpeTrainer

def train_tokenizer(data_dir, dataset_name, split, vocab_size, out_file):
    """
    Trains a HuggingFace BytePair Encoding tokenizer on sentence-pair dataset,
    saving the tokenizer representation in `out_file`
    """
    builder = tfds.builder(dataset_name, data_dir=data_dir)
    builder.download_and_prepare()
    ds = builder.as_dataset(split=split, shuffle_files=False)
    num_elems = len(ds) * 2 # yield one sentence at a time
    ds = ds.batch(1000)

    def convert(ds):
        # decode
        it = ds.as_numpy_iterator()
        decode = np.vectorize(lambda x: x.decode())
        while True:
            item = next(it, None)
            if item is None:
                return
            one, two = item.values()
            yield decode(one)
            yield decode(two)

    tokenizer = Tokenizer(BPE(unk_token='[UNK]'))
    special_tokens = ['[UNK]', '[PAD]', '[EOS]', '[BOS]']
    trainer = BpeTrainer(vocab_size=vocab_size, special_tokens=special_tokens)
    tokenizer.pre_tokenizer = pre_tokenizers.ByteLevel(add_prefix_space=False)
    tokenizer.train_from_iterator(convert(ds), trainer, num_elems)
    tokenizer.add_special_tokens(special_tokens)
    tokenizer.save(out_file)

Dataset Tokenization

The next step in the pipeline is to create a tokenized dataset using the previously trained tokenizer stored in tokenizer_file. Similar to the training process, this consumes the dataset in batches of 1000 for efficiency using tokenizer.encode_batch and np.vectorize to perform unicode decoding of the bytes data. It encodes the tokens using uint16 for space efficiency.

def token_dataset(download_dir, dataset_name, split, tokenizer_file, nproc):
    """
    Create a tokenized tf.Dataset from `dataset_name` and `split`
    Use `tokenizer_file` to initialize a tokenizer
    """
    tokenizer = data.get_tokenizer(tokenizer_file)
    builder = tfds.builder(dataset_name, data_dir=download_dir)
    # the download_dir argument of download_and_prepare seems to be ignored in favor
    # of tfds.builder(data_dir=...)
    builder.download_and_prepare()
    ds = builder.as_dataset(split=split, shuffle_files=True)
    num_elem = len(ds)
    ds = ds.batch(1000)

    def gen(ds):
        it = ds.as_numpy_iterator()
        unicode_decode = np.vectorize(lambda x: x.decode())
        while True:
            item = next(it, None)
            if item is None:
                return
            one, two = item.values()
            one = tokenizer.encode_batch(unicode_decode(one))
            two = tokenizer.encode_batch(unicode_decode(two))
            yield from [(
                tf.constant(a.ids, dtype=np.uint16),
                tf.constant(b.ids, dtype=np.uint16))
                for a, b in zip(one, two)]
    return gen(ds), num_elem

Serialization using TF-Records

The next step is to serialize the tokenized dataset to disk using TF-Records (Protobuf) messages. This step consumes the tokenized dataset as a generator. Note that the data are serialized using the tf.train.Feature with the bytes_list field. Although it would be nice to directly encode using uint16, there is no such datatype available in Protobuf. Raw bytes conserve space.

Also note that it is recommended to shard the data into multiple files for reading efficiency.

def write_records(data_gen, num_elem, path_template, num_shards, shards=None):
    """
    Transform all records in ds, writing them to `num_shards` separate
    `path_template` files.

    ds:  tokenized dataset
    path_template:  a relative or full path including filename stub
    num_shards:  how many separate tfrecord files to produce
    shards: iterable of shard numbers if specific shards are desired
    """
    options = tf.io.TFRecordOptions(
            compression_type=None,
            input_buffer_size=10000,
            output_buffer_size=10000)

    shards = range(num_shards)
    chunk_size = num_elem // num_shards
    begs = [chunk_size * i for i in range(num_shards)]

    chunk = -1
    for i, (t1, t2) in enumerate(data_gen):
        if chunk != i // chunk_size:
            chunk = i // chunk_size
            record_path = path_template.format(chunk)
            print(f'Writing chunk {chunk} to {record_path} of {num_shards} shards')
            file_writer = tf.io.TFRecordWriter(record_path, options)

        s1 = tf.io.serialize_tensor(t1)
        s2 = tf.io.serialize_tensor(t2)
        b1 = tf.train.BytesList(value=[s1.numpy()])
        b2 = tf.train.BytesList(value=[s2.numpy()])

        example = tf.train.Example(
            features=tf.train.Features(feature={
                'x': tf.train.Feature(bytes_list=b1),
                'y': tf.train.Feature(bytes_list=b2)
                }
            )
        )
        record_bytes = example.SerializeToString()
        file_writer.write(record_bytes)

Once the data have been serialized to disk in this particular way, it must be deserialized using a matching Protobuf schema. This is achieved as:

def parse_example(swap, example):
    schema = {
            'x': tf.io.FixedLenFeature([], tf.string),
            'y': tf.io.FixedLenFeature([], tf.string),
            }
    record = tf.io.parse_single_example(example, schema)
    return parse_record(swap, record)

def parse_record(swap, record):
    # see https://colab.research.google.com/notebooks/tpu.ipynb#scrollTo=LtAVr-4CP1rp&line=26&uniqifier=1
    # print(f'example[x]: {example["x"]}')
    x = tf.io.parse_tensor(record['x'], out_type=tf.uint16)
    y = tf.io.parse_tensor(record['y'], out_type=tf.uint16)
    x = tf.cast(x, tf.int32)
    y = tf.cast(y, tf.int32)
    if swap:
        x, y = y, x
    # tf.print(x)
    return { 'inputs': x, 'targets': y }

def load_tfrecord_dataset(tfrecord_glob, swap_inputs_targets):
    # optimization advice from https://codelabs.developers.google.com/codelabs/keras-flowers-data#4
    filenames = tf.io.gfile.glob(tfrecord_glob)
    if len(filenames) == 0:
        raise RuntimeError(
                f'load_tfrecord_dataset: '
                f'Couldn\'t find any files in tfrecord_glob pattern \'{tfrecord_glob}\'')

    AUTOTUNE = tf.data.AUTOTUNE
    ignore_order = tf.data.Options()
    ignore_order.experimental_deterministic = False

    dataset = tf.data.TFRecordDataset(filenames, num_parallel_reads=AUTOTUNE)
    dataset = dataset.with_options(ignore_order)
    fn = functools.partial(parse_example, swap_inputs_targets)
    return dataset.map(fn, num_parallel_calls=AUTOTUNE)

Adding Special Tokens

Since the encoder simply computes an embedding for an entire sentence, there is no need to add any special tokens to its input. For the decoder, I used the pattern BOS CONTENT EOS EOS. With just two EOS tokens at the end, this is sufficient for the decoder to learn that EOS only ever transitions to EOS and nothing else. While this transition is strictly not necessary for beam search, it does serve as a convenient positive control for debugging, since one can then sample directly from the model and see that this trivial 'rule' is being learned quickly.

During inference, the decoder input is seeded with the BOS token. This is necessary because, architecturally, the decoder generates a token by producing a query from the right-most current input. Thus it is not capable of generating a token in unseeded fashion. In other words, in the autoregressive formulation P(token | generated_seq, encoder_embedding), The length of generated_seq cannot be zero.

On-the-fly Batched Sentence Packing

The training data consist of English/German sentence pairs of widely varying lengths, as illustrated in the cartoon above. This creates a problem for training since XLA works most efficiently with fixed-sized tensors. So it is desirable to pack variable-length input and target sentences end-to-end in each batch so as not to waste compute. These lengths are the command-line argunents max_source_len and max_target_len.

The packing must be done on-the-fly to achieve novel batches of data. A first might be to greedily add the next input/target pair if both sentences fit, or start a new pack otherwise. But this is not optimal. The approach I took was to keep a large set of candidates which can be tried multiple times to fit in a given batch. In the following section I'll show the code to achieve this. In the next, I'll describe the masking and auxiliary information needed to train the model on these packs as if they were single input/target pairs.

The challenge posed by variable-length sentences

The packing step consists of consuming an individual sentence pair, testing if it fits in the remaining space of the pack, and if so, adding it to the pack. If directly implemented, this would lead to branching in the code. I opted instead to use fixed physical sizes and varying logical sizes. The approach is best explained using single sentences instead of sentence pairs.

First, each input sentence is padded to the pack length. Let's assume the pack length is 100, so that seq1.shape = [100], seq2.shape = [100] etc. But, the actual sentence token length is given as well.

The input dataset of sentences with their 'use lengths' would look like this for example:

(seq1, 27)
(seq2, 16)
(seq3, 45)
(seq4, 38)
(seq5, 18)
(seq6, 23)
(seq7, 38)
(seq8, 19)
(seq9, 47)
(seq10, 23)

The approach is to consume these inputs in the generator, while keeping track of available space in a logical pack (of length 100). The generator would alot a fixed number num_tries of attempts to add another sentence to the pack. If the next available sentence fits, it would be yielded together with its length. If not, it would be yielded together with a 0 indicating it is not to be packed.
Assuming num_tries = 5 for example, this generator would yield:

(seq1, 27)
(seq2, 16)
(seq3, 45)
(seq4, 0)  # pack is at 88, length 38 doesn't fit
(seq5, 0)  # pack is at 88, length 18 doesn't fit.  this is last try, pack remains at size 88
(seq4, 38) # new pack.  seq4 still in buffer
(seq5, 18) # seq5 still in buffer
(seq6, 23)
(seq7, 0)  # pack is at 79.  seq7 length of 38 doesn't fit
(seq8, 19) # final pack size is 98
(seq7, 38) # seq7 still in buffer.
(seq9, 47)
(seq10, 0) # pack is at 85.  seq10 length of 23 doesn't fit
...

The next transformation consumes these records in batches of 5 (num_tries) and outputs a single pack for each. Internally, the packing function uses tf.cumsum on the accompanying lengths to compute offsets and lengths for tf.tensor_scatter_nd_update. The sequences which have a zero accompanying length are naturally ignored, but they don't require any branching code.

Both of these steps are done on batches of sentence (pairs) for throughput efficiency. The key functions are shown below. In this code, the indices b, p and o respectively stand for batch, try number, and sequence length (for historical reasons). So, in the example above, p corresonds to num_tries.

@tf.function
def get_scatter_inds(batch_inds, seqs, lens):
    """
    batch_inds: pbo, a materialized tensor holding value b at index pbo
    seqs: pbo
    lens: pb

    returns: pbo2  last slice is [B,O] coordinates
    """
    O = tf.shape(seqs)[2]
    lens = lens[:, :, None]
    o_rang = tf.range(O)[None, None, :]
    begs = tf.cumsum(lens, axis=0, exclusive=True)
    pre_inds = tf.add(begs, o_rang)
    mask = tf.greater(lens, o_rang)
    inds = tf.where(mask, pre_inds, O) # B,P,O
    slice_shape = tf.shape(inds)
    return tf.stack([batch_inds, inds], axis=3)

@tf.function
def pack_values(scatter_inds, pad_value, values):
    """
    scatter_inds: pbo2
    values: pbo
    dest: bo

    Performs the operation:
    dest[*inds[p,b,o]] = values[p,b,o]
    """
    B = tf.shape(values)[1]
    O = tf.shape(values)[2]
    dest = tf.fill((B,O+1), pad_value)
    return tf.tensor_scatter_nd_update(dest, scatter_inds, values)[:,:O]

The upstream step is the dataset implemented with tf.data.Dataset.from_generator and must keep track of the current pack size with each "try". It also maintains an internal buffer of token sequences which is refilled when it falls below batch_size (corresponding to index b above). At any given try, a different subset of the b sequences in the buffer may be used or not. A buffer update step re-gathers the unused sequences and pushes them within the slots [0, b). When the buffer size falls below batch_size, the generator calls next on its upstream data to fetch another b unpacked sentence (pairs).

The full generator function is complex and can be seen here. For a flavor of what is happening, here is a snippet. In this code, used is a boolean tensor of size b which signifies which of the sentence pairs fit in the corresponding pending pack. get_condense_inds then finds the inverse of that (those sentence pairs to copy), and generates a set of indices for tf.gather_nd to copy the unused ones. In the example above, a sentence that was "used" would have an accompanying 'use length' equal to the actual sentence token length, or zero if it was unused in this 'try' iteration.

    def get_condense_inds(used):
        """
        used: b  (boolean tensor indicating which sentences were used)
        """
        used = tf.concat((used, tf.fill(batch_sz, False)), axis=0)
        copy = tf.where(tf.logical_not(used))[:,0]
        fill = tf.constant(2*batch_sz-1, shape=2*batch_sz, dtype=tf.int64)
        return tf.concat((copy, fill), axis=0)[:2*batch_sz,None]

    def condense(inds, buf):
        return tf.gather_nd(buf, inds)

There is a different approach to sentence pair packing taken in the seqio library (trim_and_pack_dataset, adapted from tensor2tensor). The approach they use is compilable to a tf.Graph, unlike mine. It may not achieve the same level of packing efficiency. By design, it consumes a certain number of sentence pairs, and must use all of them to form a variable number of packs. My approach can indefinitely delay usage of any given sentence pair. And, there is a tunable parameter num_tries which will generally increase packing efficiency for higher values.

Masking packed training pairs

To make it appear to the model as single input-target pairs, some subtle masking and careful treatment of position embedding is required.

A basic batch is a set of batch_ndim0 row pairs of lengths max_source_len and max_target_len respectively. The content of the row pair are k input-target pairs. For example for k=3 we could have:

The above cartoons show three masks. Each mask has a query and a target dimension. The query dimension corresponds to the query (output) position of the attention layer, while the target corresponds to the key or value (input) position. Each mask operates on the attention matrix, zeroing out the component where the mask is black.

On the left is the mask for each Encoder self-attention layer. It allows tokens in a given sentence to attend to each other, but not to other sentences. In the middle is the Decoder-to-Encoder cross attention. It is also bidirectional and allows any token in the Decoder sentence (the target translation sentence) to attend to any token in the matching source sentence in the encoder. Finally, the Decoder self-attention mask is a combination of the so-called 'causal' mask and a block-structured mask. In this case, it allows any query position to attend only to query positions in the same sentence and at or before the target position.

Some Tricky parts

Correctly masking padding tokens

The cross entropy loss is computed as an average over each active (non-padding) token in the packed batch of target sentences. Even though the model layers mask out padding during the forward pass, the loss must additionally be masked for padding tokens. The masking within the model prevents padding tokens from contributing to the activations of the model. The masking of the loss terms corresponding to padding targets prevents them from contributing to the gradient. I forgot to mask the loss terms in an earlier version of this work. I don't recall exactly the shape of the loss curve, but it did train decently well, but failed to reach reported performance in the paper.

Gradient Accumulation and varying batch size

I did my training runs on TPU with batch_dim0=96 and max_target_len=320, which resulted in about $27,000 \pm 500$ target tokens per batch. This is slightly larger than the published base model run of $50,000$ source + target tokens.

The 96 sentence pairs were divided first by shards assigned to each TPU core, then gradient accumulation steps, as: 96 = 8 shards x 2 steps * 6 sentence pairs. The approach I took is to compute sums of gradients, first across steps, then cores. Finally, normalize by the total number of active loss terms.

The accumulate_gradient function is shown below.

def accumulate_gradient(loss_fn, params, data, shard_size, rng):
    """
    Applies loss_fn (and gradient) to `shard_size` chunks of leading dim of data
    and returns the sum
    """
    # returns (loss, metrics), grad
    grad_fn = jax.value_and_grad(loss_fn, has_aux=True)
    grad_fn = functools.partial(grad_fn, params)

    def reshape_fn(x):
        return jnp.reshape(x, (x.shape[0] // shard_size, shard_size, *x.shape[1:]))
    data = jax.tree_map(reshape_fn, data)
    accu, rng = jutils.map_sum(grad_fn, data, rng)
    (_, metrics), grad = accu
    return metrics, grad

In particular, it is important to feed in a different rng for each gradient accumulation step, which is used as a seed for hk.dropout layers. It uses jutils.map_sum, a convenience wrapper around jax.lax.scan. It applies a function to each slice of data, and then sums the slices. It overcomes the problem of getting the shape of the first application of the function.

def map_sum(map_fn, data, rng):
    """
    Maps map_fn across the items of data (split by the leading axis)
    Returns: sum of mapped items, new_rng

    Inputs:
        data: a pytree of tensor leaves.  Each tensor has the same sized axis 0
        rng:  random seed
        map_fn:  (data_slice, rng) -> result
                 where data_slice is a pytree of one slice along axis 0 of each
                 leaf of `data`
    Returns:
        sum of each result returned by map_fn
    """
    initial_data = jax.tree_map(lambda x: x[0], data)
    result_shape = jax.eval_shape(map_fn, initial_data, rng)
    result = jax.tree_map(lambda dst: jnp.zeros(dst.shape, dst.dtype), result_shape)
    rng, = jax.random.split(rng, 1)
    carry = result, rng

    def scan_fn(carry, item):
        accu, rng = carry
        result = map_fn(item, rng)
        rng, = jax.random.split(rng, 1)
        accu = jax.tree_map(lambda x, y: x + y, accu, result)
        carry = accu, rng
        return carry, 0

    carry, _ = jax.lax.scan(scan_fn, carry, data)
    return carry

Beam search

The beam search routine maintains a set of live sequences (not ending in EOS) and completed sequences (ending in EOS). At each step, it creates a cartesian product of num_live * n_vocab extension sequences by extending each live sequence with each of the possible tokens. It then applies the local scoring function, which in LLMs is simply $\log P(\text{seq})$ to each of these extended sequences, and selects the top $2k$ of them.

Starting from $k$ distinct live sequences, it is guaranteed that there will be at least $k$ of the top $2k$ extensions that are also live. This is because at most $k$ of the extensions can end in EOS (one for each distinct live sequence). The algorithm thus selects the top $2k$ from the extension set to guarantee at least $k$ live sequences available at each step.

Any of the top $2k$ scoring extension sequences that happen to be complete are then combined with the existing completed sequences. Then, the top $k$ of these, according to a global scoring function are selected and retained, The global scoring function must have some quality that allows it to directly compare sequences of different length. In general, the local scoring function can only reliably compare sequences of identical length.

def beam_search(beam_size, n_vocab, steps, local_score_fn, global_score_fn):
    BOS = 0  # begin-of-sequence token
    EOS = 1  # end-of-sequence token
    k = beam_size             

    toks = list(range(n_vocab))
    live  = list([BOS])         # live sequences (not ending in EOS)
    comp  = list()              # completed sequences (ending in EOS)

    by_score = lambda el: -el[1]

    for _ in range(steps):
        exts = [ (l + [t], local_score_fn(l + [t])) for l in live for t in toks ]
        best = [ e for e,_ in sorted(exts, key=by_score)[:2*k] ]
        live = [ l for l in best if l[-1] != EOS ]
        newc = [ l for l in best if l[-1] == EOS ]
        if len(newc) == 0:
            continue
        # refresh comp
        cand = [ (c, global_score_fn(c)) for c in newc + comp ]
        comp = [ c for c,_ in sorted(cand, key=by_score)[:k] ]

    return comp

Jax implementation detail

In jax, a few optimizations are employed. First, the cartesian product exts is never materialized. Disregarding the batch dimension, this would be a tensor of shape [l*v,s+1] and waste a lot of memory. Rather, the scores are computed with shape [l,v], then flattened and the top-k selected from them. best is constructed by gathering both the live sequences and matching token extensions using the same index set, then concatenating.

Second, instead of variable-sized tensors to represent the current live and cand sets, I use fixed sizes, and represent missing sequences with score of negative infinity, which are naturally ignored in the top-k selections.

All inference steps are incremental and employ a decoder key-value cache, which exists for every layer of the decoder. Also, the global score function requires a tally of total attention paid to each position from the encoder. This tally is specific to each live sequence. It must be incrementally updated at each step, and separately, the entries corresponding to the selected live sequences must also be gathered.

Finally, the step to refresh the comp tensor is only performed if there are any new completed sequences. This is accomplished using jax.lax.cond to conditionally execute the refresh function.

See beam_search_step for details.

Pre- vs Post- style layer normalization

I tried the originally described architecture in which layer normalization is done at the end of a layer, as well as the Pre-LN form. Explicitly in the case of an encoder-decoder architecture, these two forms (ignoring layer parameters) are:

def attn(kvinput, qinput, qtmask=None):
    """
    Q = query context length
    T = target context length
    M = model embedding dimension
    kvinput: [T,M] - embedding vectors for keys/values
    qinput:  [Q,M] - embedding vectors for queries
    qtmask:  [Q,T] - which queries can attend to which targets
    """
    pass

def pff(embed):
    """
    embed: [Q,M] - embedding vector sequence
    Outputs position-wise feed-forward
    """
    pass

# Original architecture
# Output of each layer
def orig_model(x, y):
    for _ in range(6):
        x = norm(x + dropout(attn(x, x)))
        x = norm(x + dropout(pff(x)))
    for _ in range(6):
        y = norm(y + dropout(attn(y, y, causal_mask)))
        y = norm(y + dropout(attn(x, y)))
        y = norm(y + dropout(pff(y)))
    return y

# Pre-LN architecture
# Embeddings normalized just before input to attn or pff
# Main stream not normalized
def preln_model(x, y):
    for _ in range(6):
        x = x + dropout(attn(norm(x), norm(x)))
        x = x + dropout(pff(norm(x)))
    for _ in range(6):
        y = y + dropout(attn(norm(y), norm(y), causal_mask))
        y = y + dropout(attn(norm(x), norm(y)))
        y = y + dropout(pff(norm(y)))
    return y

Encoder Positional collapse

The original architecture trained well, to a train set perplexity around 6. And, it yielded decent translations. However, before I went further I noticed that the beam search beta parameter had no effect. This turned out to be because the encoder output embedding vectors were nearly identical along all positions in the input context.

To figure out why, I looked at the outputs of all layers in the encoder for a given input, and found that the individual embedding vector positions became more and more similar and were within about 1% value by layer 4. I believe this form of "collapse" might be an intrinsic feature of bidirectional self-attention. Since every output position of such a layer is a convex combination of its inputs (before a linear transformation), this implies that, taken together, the collection of output positions' convex hull will be interior to the convex hull of the collection of input positions. Thus, repeated application of these will result in irreversible shrinking of the hull to a point.

The only thing that can stop this shrinking is the addition of the main input. However, it turned out that the L2 norm of the residual term dropout(attn(x, x)) was 2-4 times greater than that of the main term x. Thus, I believe, the shrinking behavior of the attention wins out, resulting in this 'collapsing' behavior across positions.

This phenomenon completely disappears in the Pre-LN architecture. On the face of it, this makes sense because normalizing only the input to the self-attention operation, attn(norm(x), norm(x)), will limit its contribution relative to the main term x.

Layer Norm causal leakage

Initially, I was incorrectly applying layer norm across both the Q and M dimensions (see pseudo-code above). This was a subtle bug - it turns out it creates information leakage that violates the auto-regressive property in the decoder, which manifests as suspiciously fast training down to zero loss. To assess this, I used jax.vjp function (vector Jacobian product) to test gradients of the decoder with respect to each position of input embeddings. Various ablation experiments narrowed down the culprit to the LayerNorm. See tests/layernorm_leakage.py. The solution was to apply LayerNorm only to the M axis.

Regularizing aggregate Attention distribution over targets

One aspect of attention layers is there is no structural mechanism for query positions to coordinate among themselves. The output at some query position $q_1$ is an independent computation from that at $q_2$. In particular, both queries could produce very similar attention weights across the target space, despite positional encodings.

Where this happens, it seems undersirable from the following perspective. Suppose we interpret the outputs of attention as explanations, and the inputs as observations. An explanation attending to a subset of those inputs is interpreted as explaining those inputs. Under this interpretation, it is desirable for all inputs to be sufficiently explained, and for any given observation not to have too many explanations.

In an extreme case, if a particular observation has no explanation (it has not been attended to by any query), then it is ignored by the network and will not affect the output. In this particular task of sentence translation, that is a priori a bad thing since the nature of the task calls for all aspects of the input sentence to influence the translation.

The situation of maximal explanation over the observations is one in which each observation collectively receives the same amount of attention from all query positions across all heads. Intuitively this can be measured from the attention matrix $A$:

$$\begin{aligned} T & \equiv & \text{number of target positions} \\ M_t & = A_{hqt} & \text{aggregate over heads and query positions} \\ Z & = A_{hqt} & \text{total attention} \\ p_t & = M_t Z^{-1} & \text{normalize} \\ S & = H(p) (\log T)^{-1} & \text{scaled attention entropy} \end{aligned}$$

Adding the loss term $(1 - S)^2$ to training results in a very slight improvement in Bleu scores across checkpoints. This is not very apparent in the plots, but taking a checkpoint-matched difference reveals a clear pattern.

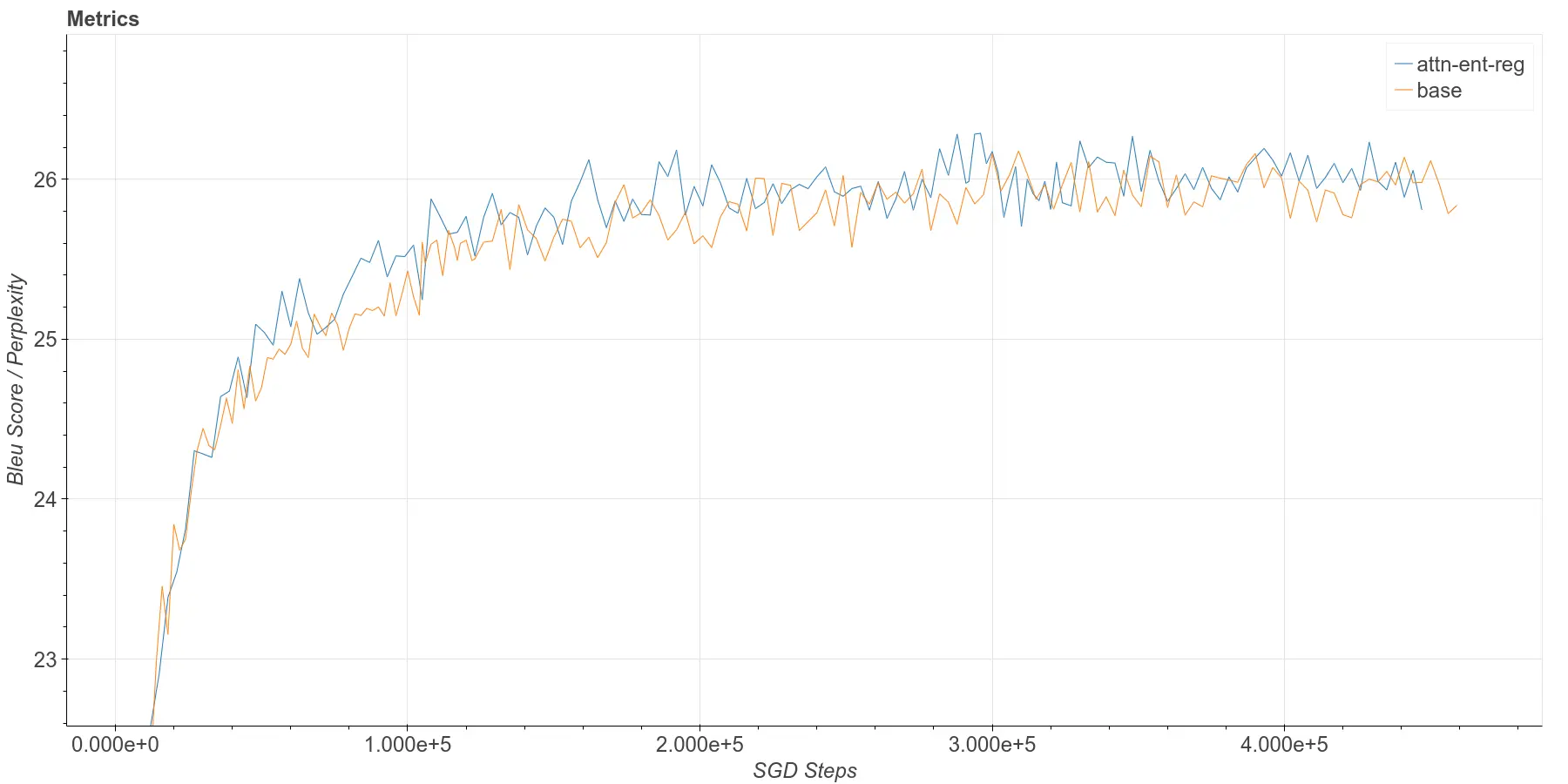
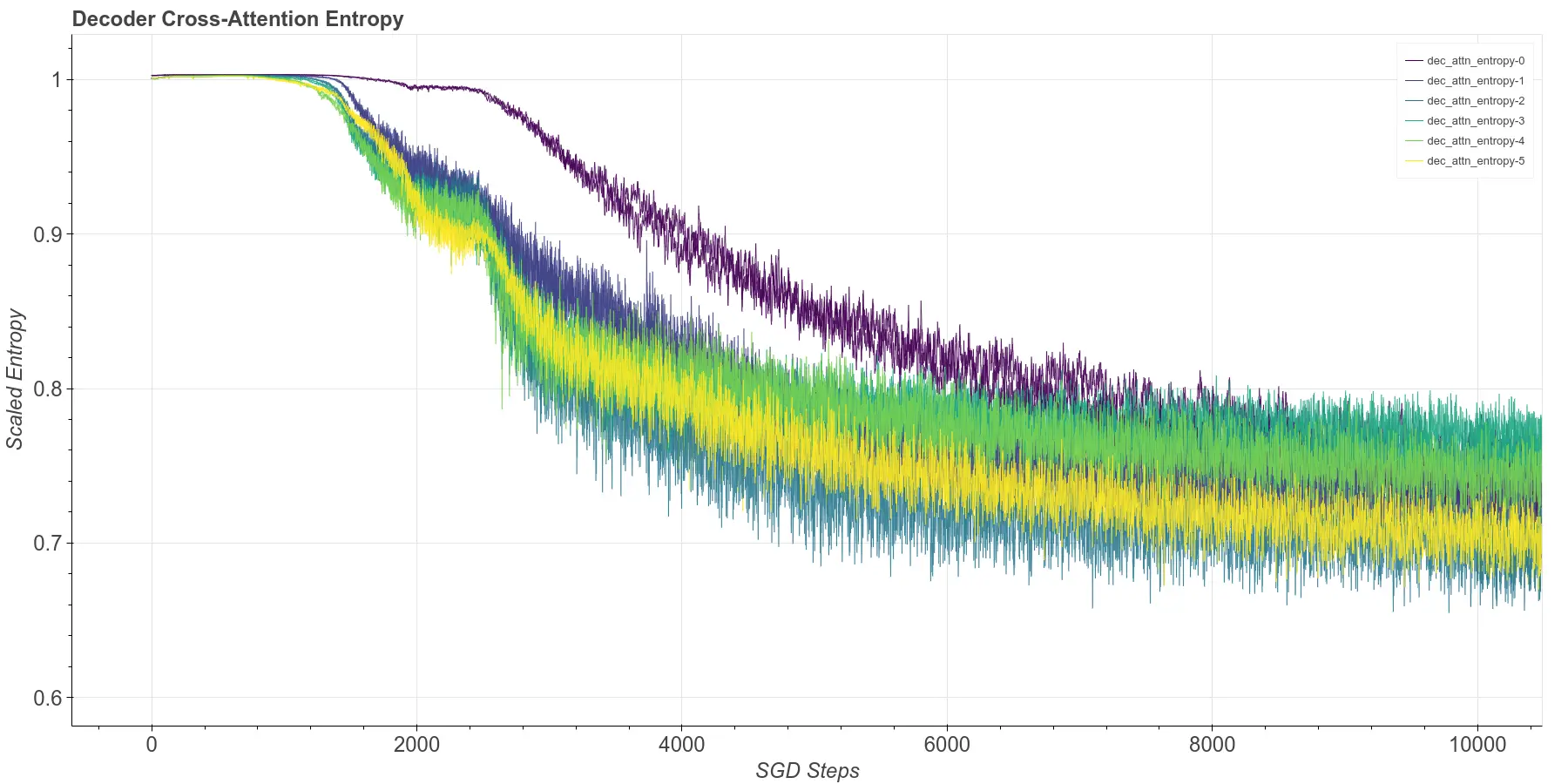
A complete side-by-side comparison of attention entropy plots can be seen here. Below, I show zoomed view of the first 10k training steps for the Decoder cross-attention entropy. In it, you can see that the unregularized case starts to head for the $[0.6, 0.8]$ range, while the regularized case starts to converge to $[0.99, 1.0]$.

One question is whether it is desirable to encourage more uniform attention to the targets in each layer. From a learning theory point of view, adding a loss term to encourage this is a form of regularization. It restricts the model search space to those models which "achieve" this uniform attention. If this can be done without sacrificing perplexity (or with a favorable tradeoff), it may help.

Some initial confusion on Perplexity in the presence of label smoothing

There are two conflicting definitions of perplexity online. For instance, HuggingFace correctly defines the PPL formula here, but then, ambiguously, goes on to say:

[Perplexity] is also equivalent to the exponentiation of the cross-entropy between the data and model predictions.

and go on to link to a blog post that states the same. Just to clarify, it is understood that cross-entropy is in conditional form $H(q(x_t|x_{<t}), p(x_t|x_{<t}))$, where I take $q$ to represent the data distribution and $p$ the model distribution. But, what is meant by data distribution here is ambiguous. It could mean the empirical measure (i.e. one-hot distribution implied by the token at a particular $t$), or it might mean the distribution created from the label smoothing.

If you view label smoothing as not part of the data distribution, then the statement is true. In any case, in this paper, I can verify that the formula used which achieved a PPL value of 4.92 on the dev set (newstest2014) was the one using data distribution as empirical measure, even though they use label smoothing in the actual cross-entropy objective. The following section shows both:

# p[t,v]  - model probability of token v at position t
# q[t,v]  - data  probability of token v at position t (could be either one-hot or softened)
# tok[t]  - the actual token at position t
ppl_formula_used_in_paper  = 2 ** - ((1/T) * sum(log2(p[t,tok[t]]) for t in range(T)))
often_reported_ppl_formula = 2 ** - ((1/T) * sum(q[t,v]*log2(p[t,v]) for t in range(T) for v in range(V)))

What to ignore, and when?

While the specific task of translation might demand that every piece of input context be paid attention to, this is not the case for language modeling tasks in general. For instance, in a question answering task, parts of the question might be irrelevant to the answer, and so forth. So it would seem the primary purpose of attention would be to learn when to ignore irrelevant information. But, where in the network would this ignoring happen?

Concretely, suppose you have a decoder-only model, and a question-answering training example that has some stretch of context that is completely irrelevant to the answer. Clearly, the very first layer of the network could not (and should not) ignore this context. There is simply not enough processing done yet to reach a high enough level of abstraction that this would be achievable. If we imagine the very first layer as mainly recognizing words or word stems from individual tokens, there is no way that it could know in advance that whole sections of the input should be ignored.

But if not then, when? At what point in the processing does the model begin to ignore the context? One useful way to think about this is to roll out the generation process and ask what patterns of attention exist in the collective generated section from the context.